Number Puzzle

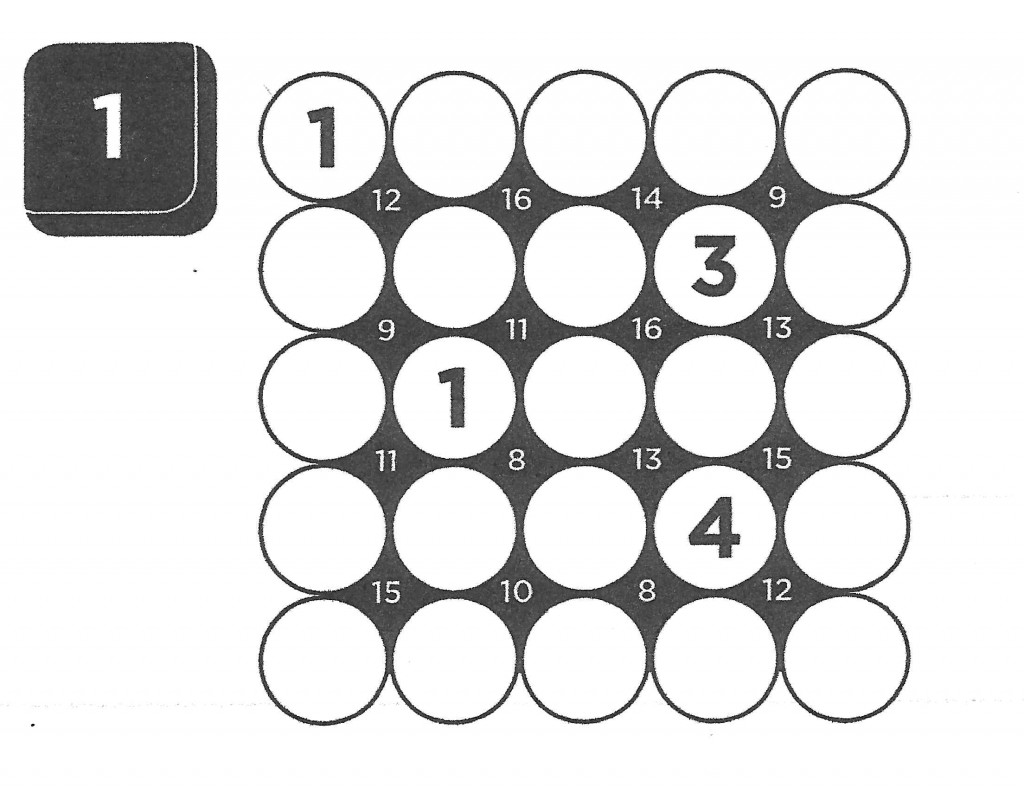
Today’s puzzle is another original puzzle called Number Junctions. I originally named these puzzles Octangles as they contained a collection of octagons. However, when Mindware published them in book form (actually two books), they changed the format to circles and subsequently the name. Number Junctions are easy to understand – all you need to do is to place the given numbers into the small following the simple rules (or directions). In order to correctly solve these puzzles, you will only need to use basic addition and your deductive reasoning skills. Each puzzle is an nxn grid (like 5×5 or 9×9) of circles. Between every group of four circles is a “diamond” containing a number. This number is the sum of the numbers in the four surrounding circles. Finally, each row (and column) contains the numbers 1 through n once and only one (just like Sudoku). You just have to place the numbers correctly into the empty circles

Click here for a detailed set of rules and an example puzzle.

Here is an easier 5×5 Number Junctions puzzles from my second book for you to try.



For a more challenge 9×9 Number Junctions puzzle click here!


If you like these Number Junctions puzzles, take a look at the books of Number Junctions that I wrote which is available on mindware. Good Luck and pass the puzzles onto others who may enjoy them!

“Today you are you!  That is truer than True!  There is no one alive that is you-er than you!” – Dr. Suess

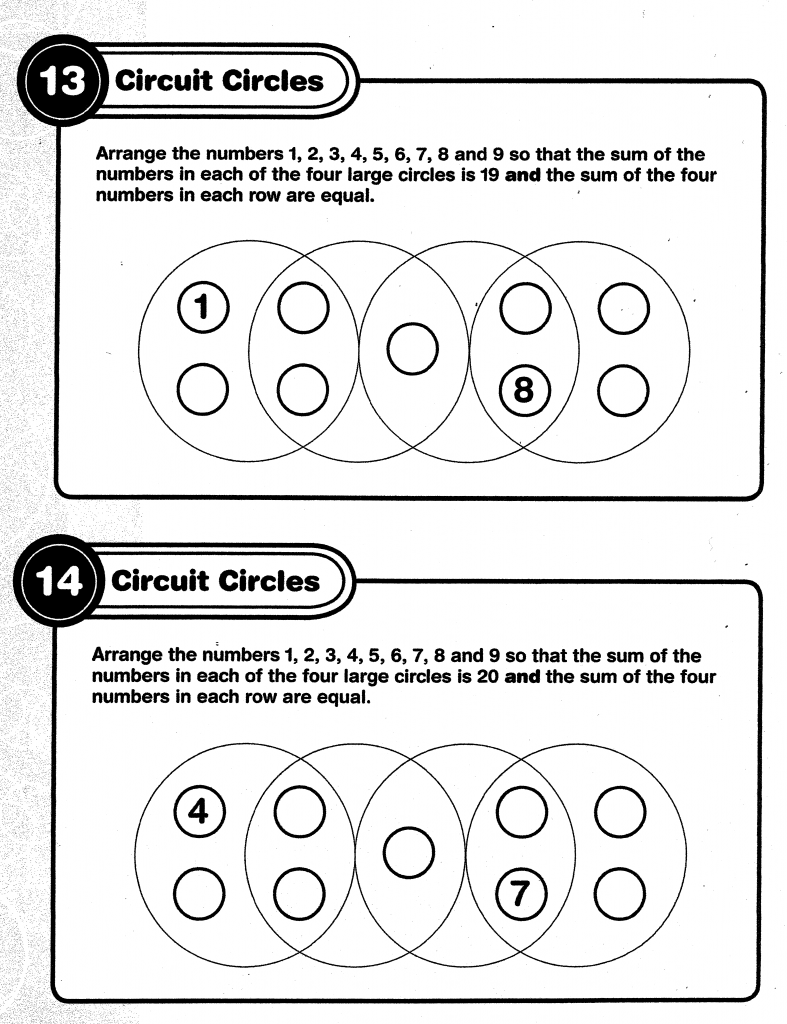
Today’s puzzle is another original puzzle called Number Circuits.  I originally named these puzzles Magic Puzzles as they are based on Magic Squares.  However, when Mindware published them in book form (acually two books), they changed the name.  Number Circuits are easy to understand – all you need to do is to place the given numbers into the small circles following the simple rules (or directions).  In order to correctly solve these puzzles, you will only need to use basic addition and your deductive reasoning skills.  

Here are two Number Circuit puzzles from my second book for you to try –   Click here for a pdf file.

If you like these Number Circuit puzzles, take a look at the books of Number Circuits that I wrote which is available on mindware.  Good Luck and pass the puzzles onto others who may enjoy them!

“” –

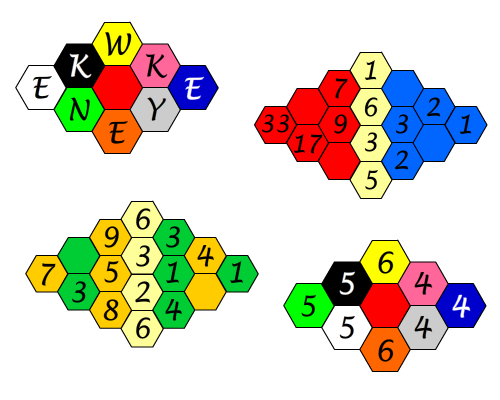
Today’s puzzles are Hex Codes.  Each puzzle is a collection of adjacent hexagons that follow a pattern.  Each hexagon contains either a number/letter or is empty.  The objective is for you to fill in empty hexagons with the correct number/letter that follows the given pattern.  You must determine the pattern that each puzzle exhibits in order to correctly complete each puzzles.  The hexagons may vary in color which may be of importance (hint, hint, nudge, nudge).  Some of the puzzles may use addition or subtraction, while others may utilize some other connection (like adjacent hexagons or the color) between certain attributes.  That’s all for you to figure out.  These puzzles can be very challenging. 

All you need to do is to figure out the pattern in each puzzle and then use it fill in empty hexagons.  Below are four puzzles to try.  If you like them, click here for a pdf file with more.  Best of luck!


As always, I hope you enjoyed these puzzles.  Please pass them onto others who may enjoy them!

“The hardest arithmetic to master is that which allows us to count our blessings.” – Eric Hoffer

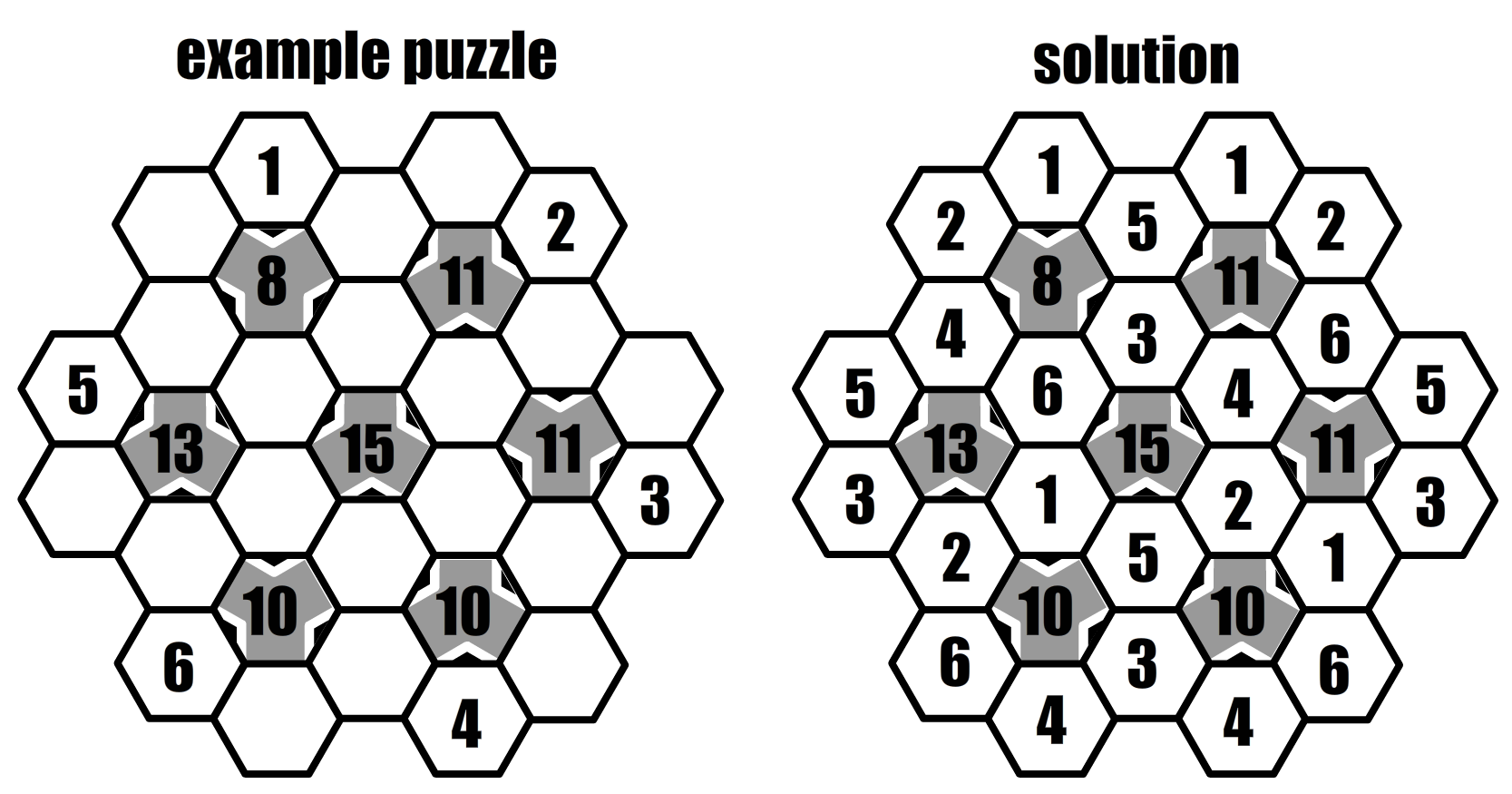
Today’s puzzle is an original puzzle idea that I named Kuruko puzzles.  (Sounds nearly exotic doesn’t it?)  In any case, these puzzles are somewhat like Sudoku puzzles in that you need to fill in empty “boxes” with numbers following a given pattern.  In Sudoku, the “boxes” are squares and they are evenly distributed in chess board-like grid.  In Kuruko, the “boxes” are hexagons and they are distributed in a hexagonal pattern.  Some of the hexagons are gray (7 of them) and some are white (24 of them).  Around each gray hexagon there are six white hexagons.  Also, three of the six white hexagons surrounding each gray hexagon “point” to the gray hexagon with a black arrow. Just like Sudoku, Kuruko has some very simple rules to follow, actually just two rules:

Rule 1. The number in each gray hexagon is the sum of the numbers in the three white hexagon pointing to it.

Rule 2. Each gray hexagon is surrounded by the numbers 1 through 6 once and only once in each of the six surrounding white hexagons.

Here’s and example puzzle and solution:

Now for the puzzles. Below are two Kuruko puzzles from my Kuruko puzzle book containing 100 original Kuruko puzzles. Just following the simple rules to solve and Good Luck!

“Believe you can and you’re halfway there.” – Theodore Roosevelt

Today’s puzzle is a great puzzle that everyone can enjoy. They are called alphametics. In each puzzle, there is a simple addition problem. However, instead of using numbers, letters are used. Each letter stands for a single digit number (e.g. 0,1,2,3,4,5,6,7,8 or 9). Within each puzzle, a number can be associated with only one letter, so two different letters can not equal the same number. The meaning of the letters may change from puzzle to puzzle, so “N” may be “5” in the first puzzle and may be “3” in the second puzzle. The objective is to assign each letter a number so the statement is correct – in other words, it all adds up. It sounds straight-forward and is easy to understand, but may be very challenging. Here’s an example:

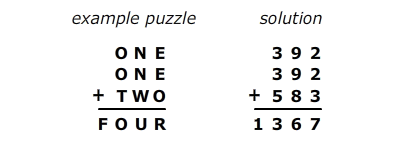
In this example, there are eight different letters each matched with a unique number, so F=1, O=3, U=6, R=7 and so on. Make sure you understand the example. When you do, try the following puzzles. I have created three interactive puzzles below.

I hope you enjoy these puzzles. Good Luck and pass the puzzles onto others who may enjoy them!

Here’s another Number Sense Puzzle. Today’s puzzle centers around another fundamental skill that gives many students a really difficult time – Order of Operations. This is geared to younger puzzlers to help them improve their Order of Operations skills. As always, let me first give a general introduction. There will be 8 statements each corresponding to a number. You have to use the numbers 0 through 9 once and only once to fill in the correct number for each statement. You will need to use and develop your deductive problem solving skills in order to correctly place the numbers. Since there are only 8 answers and 10 numbers (0 through 9), some of the answers will require two digits. In this puzzle, some of the answers will be negative, that’s no problem, just make sure the digits use 0 through 9 once and only once.

I created an interactive puzzle that will automatically check your answer and provide feedback. I also created a pdf file that can be used in classrooms or with pencils for those so inclined. The goal is to have fun and challenge yourself.

I hope you enjoy these puzzles. If you find these interesting, Click Here for a selection of more Number Sense puzzles that I’ve created. I will be adding to the selection over time. Good Luck and pass the puzzles onto others who may enjoy them!

“Lost time is never found again.” – Ben Franklin

When working with students in elementary school, I like to talk about sequences or number patterns.  I often present them with the start of a sequence, say the first three numbers.   I then ask the class to give me the next term (or number) in the sequence.  Letting everyone in the class mull it over for a bit, I ask for the pattern (the code essentially) and the next few numbers.  When I first did this, I was amazed!  I had a sequence in mind, but the students kept giving different, yet very viable sequences.  Not only that, they could justify their answers by supplying the “code” for the sequence.  I quickly realized that with just three numbers at the start of a sequence, the possibilities were plentiful.  It was quite the challenge for the students also.

So, I started doing this as a “break the ice” activity with classrooms.  We would use the same three numbers again and again, and see how many different (yet viable) sequences could be made.  When they give me a sequence and its corresponding justification, I would say “great, let’s find another” and erase it leaving only the first three “seed numbers” that I had originally written.  I  would then ask them to give me another different sequence and the whole thing would start over again.  Each time I do this, I am still amazed at how many different sequences they come up with and how challenging they find it.  Here’s the start of a sequence for you to try …

Here’s three numbers that start a sequence:    2, 3, 5, . . .

What do you think the next number can be?  How about the number after that?  Remember, it has to follow a pattern, so you can easily find each successive number by applying the pattern.

I’ve given this pattern to numerous classrooms.  Each time,  they came up with a variety of different answers, all of which make a valid sequence.  For the next number, classes have given 7,  some have given 8 while others have given 14.  In all, from all of the classes, I have received 9 different sequences that these three numbers can generate (and there’s even more!).

My challenge to you is to find as many different sequences that can be generated using the first three numbers  2, 3, 5.  Remember don’t just come up with the sequence, but identify the pattern that it follows.  Challenge yourself to see if you can find nine different sequences.  Good luck, have fun and challenge others, the more the merrier!

If you like this puzzle, click LIKE below!  Thanks.

“Go fast slowly” – Clarence Stephens

Number Circuits are an original puzzle that I came up with a few years ago.  They are number sense puzzles that require you to arrange a set of numbers in a designated pattern.  I used magic squares as a theme using shapes other than squares. In all, I was able to develop over 200 puzzles all with this same theme.  Fortunately, Mindware liked the puzzles and published two books.  I was pretty excited (and still am).  The books differ in difficulty, although neither set of puzzles are too difficult (although all puzzle are challenging when you can’t solve them!).  Below are four puzzles, two from each book.  I believe they’re representatve of each collection and Number Circuit puzzles in general.  Click each picture to open a full sized pdf image of each puzzle in a new window.

from Number Circuits A	from Number Circuits B

As always, I hope you enjoyed these puzzles. Please pass them onto others who may enjoy them and please click LIKE below if you like them! 

MIndware currently has the books for sale for only $3.95 (that a 69% savings!).  If interested in purchasing either book just click below:

Number Circuits A (Beginner Puzzles)

Number Circuits B (Advanced Puzzles)

“Some of us think that holding on makes us strong, but sometimes it is letting go.” – Hermann Hesse

Today’s puzzles are Hex Codes.  I introduced some Hex Codes during the Holiday Puzzles back in December. Each puzzle is a collection of adjacent hexagons that follow a pattern.  In today’s puzzles, each hexagon contains either a number or is empty.  The objective is for you to fill in empty hexagons with the correct number that follows the given pattern.  You must determine the pattern that each puzzle exhibits in order to correctly complete each puzzle.  The hexagons may vary in color which may be of importance (hint, hint, nudge, nudge).  Some of the puzzles may use addition or subtraction, while others may utilize some other connection (like adjacent hexagons or the color) between certain attributes.  That’s all for you to figure out.

Below are two Hex Code puzzles for you to try.  All you need to do is to figure out the pattern in each puzzle and then use it to fill in the empty hexagons.  The puzzles are different codes so the colors have different meaning within each puzzle.  Best of luck!

Puzzle 1

Puzzle 2

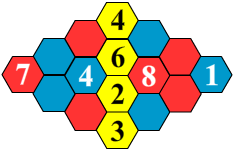
As always, I hope you enjoyed these puzzles.  Please pass them onto others who may enjoy them and please click LIKE below if you like them!

“Begin doing what you want to do now. We are not living in eternity. We have only this moment, sparkling like a star in our hand and melting like a snowflake.” – Francis Bacon

This is a new puzzle that is an extension of the Kuruko Puzzles that I created. Like Kurulko puzzles, they are similar to Sudoku puzzles.  I call them Snowflake puzzles because of their shape.  Snowflakes are symmetric shapes with six points.   The Snowflake puzzle follows this design.  It is comprised of 42 hexagons (six sided shapes).  There are white and yellow hexagons.  To complete the puzzle you must fill in each of the empty white hexagons.  There are two simple rules to follow:

1. Surrounding each yellow hexagon there are six white hexagons, these must contain the numbers 1 through 6 (each number once and only once)

2. The number in each yellow hexagon is the sum of the numbers in the three white hexagons that point to it (with a black triangle).

Here’s a snowflake puzzle for you to try –   Click here for a pdf file.

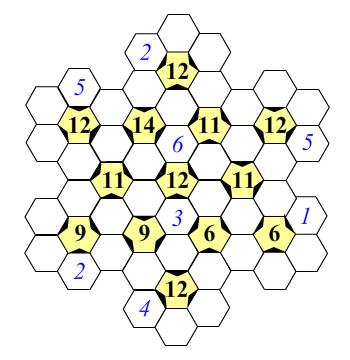
If you like the snowflake puzzle, take a look at the book of 100 Kuruko Puzzles that I wrote which is available on Amazon.com.  Good Luck and pass the puzzles onto others who may enjoy them!