“Begin doing what you want to do now. We are not living in eternity. We have only this moment, sparkling like a star in our hand and melting like a snowflake.” – Francis Bacon
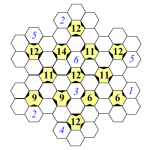
Today’s puzzle is called a Snowflake Puzzle. This is an extension of the Kuruko Puzzles that I created. Like Kurulko puzzles, they are similar to Sudoku puzzles. I call them Snowflake puzzles because of their shape. Snowflakes are symmetric shapes with six points. The Snowflake puzzle follows this design. It is comprised of 42 hexagons (six sided shapes). There are white and yellow hexagons. To complete the puzzle you must fill in each of the empty white hexagons. There are two simple rules to follow:
1. Surrounding each yellow hexagon there are six white hexagons, these must contain the numbers 1 through 6 (each number once and only once)
2. The number in each yellow hexagon is the sum of the numbers in the three white hexagons that point to it (with a black triangle).
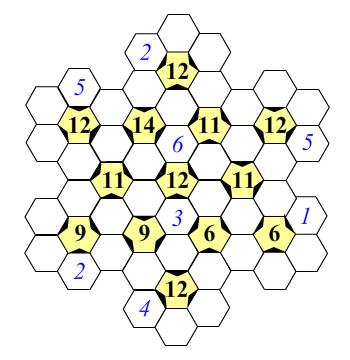
Here’s a snowflake puzzle for you to try – Click here for a pdf file.
If you like the snowflake puzzle, take a look at the book of 100 Kuruko Puzzles that I wrote which is available on Amazon.com. Good Luck and pass the puzzles onto others who may enjoy them!



