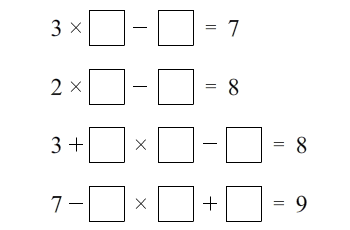Numbers

“Excellence is the gradual result of always striving to do better.” – Pat Riley

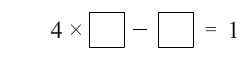
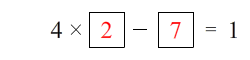
Today’s puzzle is a Number Sense Puzzle.  They are geared for younger puzzlers to help them improve their number sense.  However, many have requested more challenging puzzles, so I have included a second more challenging puzzle for older puzzlers (just click the link below). In each, there are 8 statements each corresponding to a number.  You have to use the numbers 0 through 9 once and only once to fill in the correct number for each statement.  You will need to use and develop your deductive problem solving skills in order to correctly place the numbers.  Since there are only 8 answers and 10 numbers (0 through 9), some of the answers will require two digits. 

I hope you enjoy these puzzles.  If you find these interesting, Click Here for a selection of more Number Sense puzzles that I’ve created.  I will be adding to the selection over time. Good Luck and pass the puzzles onto others who may enjoy them!

“You must be the change you wish to see in the world.” – Mahatma Ghandi

Here’s another new number sense puzzle. It’s pretty easy to explain and hopefully to understand. You’re given a start number and an end number. You have to “morph” the start number into the end number by using the provided operations and entering numbers. There are two rules.

1. digits can only be used once (at most)
2. order of operations is always left to right

Here’s an example:

You have to fill in the two “boxes” with numbers (1-digit or 2-digit numbers) so that the result equals 1. Remember, that digits can not be used more than once, so right away you know that “4” and “1” can not be in either of the two entered numbers. Below is the solution:

“4 x 2″ is 8 and then “8 – 7″ is 1.  That’s all there is to it.  Here are a few more puzzles to try:

Good luck with the puzzles and pass them along to others who may enjoy them!

“What people don’t realize is that professionals are sensational because of fundamentals” – Barry Larkin

Number sense if a fundamental skill.  I like to refer to it as “Number Familiarity“. How familiar are are you with numbers.  For example, take the number 64.  How familiar are you with the number 64?  

• – Do you know it’s a perfect square?    
  – Do you know it’s a power of 2?    
  – Do you know it’s a perfect cube?  
  – Do you know it’s the product of two perfect squares?
  

64 equals all of these – it’s 8²,   2⁶,   4³  and   (2²)(4²). 

I think that simply stated number puzzles are a great way to increase number sense.  It doesn’t matter if you’re seven or eighty-seven, concise number puzzles can be beneficial.  Here’s a few concise number puzzles to try:

1. Can you think of two numbers that when multiplied make 8 and when added make 6?
2. Can you think of two numbers that when multiplied make 32 and when added make 18?
3. Can you think of two numbers that when multiplied make 48 and when added make 14?

These puzzles should not be solved algebraically (e.g. via a system of equations).  Instead, these puzzles should stimulate thinking and making number connections.  They should also generate confidence.  There are very few things that generate confidence better than success.  Once these puzzles are mastered, change it up a bit.  Keep the puzzles generally the same, but ask for something different.  Instead of asking for the numbers, ask for the difference of the numbers, or ask for the smaller or larger number.  This adds another level of challenge to the problem.  Here are a few additional number puzzles to try:

1. What is the difference of two numbers that when multiplied make 18 and when added make 9?
2. What is the larger number of two numbers that when multiplied make 30 and when added make 13?
3. What is the smaller number of two numbers that when multiplied make 48 and when added make 19?

These puzzles are similar to the first set of puzzles, but differ as they are more challenging because the two numbers must be further manipulated to obtain the correct answer.  Continuing this theme of making the puzzles more challenging, here are a few more number puzzles to try:

1. Can you think of two numbers that when multiplied make 16 and adding one number to twice the other makes 8?
2. Can you think of two numbers that when multiplied make 24 and adding one number to twice the other makes 14?
3. Can you think of two numbers that when multiplied make 36 and adding one number to three times the other makes 21?

These puzzles will help build fundamental number sense.  They can be easily stated, understood and quickly solved.  They serve as great 1-minute problems and can assist in building confidence which will lead to even better problem solving skills.  Give them a try and share them if you like them.  Have fun and good luck!

“There are three kinds of people: Those that make things happen, those that watch things happen and those that wonder what happened. ” – Agent Garbo (Juan Pujol Garcia)

 Prime numbers are everywhere and they are really easy to understand.  There are just two simple rules to follow:

• a prime number is a positive integer greater than 1
• a prime number is evenly divisible by only 1 and itself

That’s pretty straight forward.  Many people assume 1 is a prime number, but by definition, it’s not.  It’s important to realize and remember this when dealing with primes.  Also, 2 is the only even prime number, as all other even numbers are divisible by 1, 2 and itself.

Here’s a couple of prime number puzzles to start you off. 

puzzle 1: What is the smallest 2-digit prime number in which both digits are prime and their sum is prime? 

puzzle 2: What is the largest 2-digit number in which both digits are prime and their sum is prime?

Let’s look at an example number, say 73.  73 is a prime number and it’s digits, 7 and 3 are both  prime.  However, the sum of the digits 7+3 equals 10, which is not prime.  So, 73 will not work for either puzzle 1 or puzzle 2.

Once you solve the first two puzzles, you should have a good handle on prime numbers.  I recommend listing all of the prime numbers less than 100.  To make it a bit more challenging, let’s look at 3-digit numbers.

puzzle 3: List all 3-digit numbers that have prime numbers for all three digits. 

puzzle 4: Of the numbers listed in puzzle 3, list the numbers in which the digits sum to a prime number.

puzzle 5: Of the numbers listed in puzzle 4, which of the numbers are themsleves prime?

Let’s look at an example 3-digit number, say 235.  the digits, 2, 3 and 5, are all prime numbers.  However their sum, 2+3+5, equals 10, which is not a prime number (so it doesn’t work for puzzle 4).

Good luck with the puzzles and have fun.