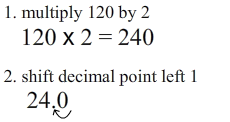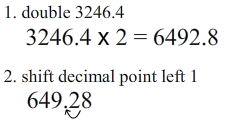Math

“You must be the change you wish to see in the world.” – Mahatma Ghandi

Here’s another new number sense puzzle. It’s pretty easy to explain and hopefully to understand. You’re given a start number and an end number. You have to “morph” the start number into the end number by using the provided operations and entering numbers. There are two rules.

1. digits can only be used once (at most)
2. order of operations is always left to right

Here’s an example:

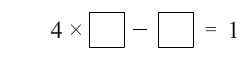
You have to fill in the two “boxes” with numbers (1-digit or 2-digit numbers) so that the result equals 1. Remember, that digits can not be used more than once, so right away you know that “4” and “1” can not be in either of the two entered numbers. Below is the solution:

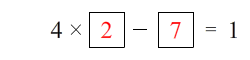
“4 x 2″ is 8 and then “8 – 7″ is 1.  That’s all there is to it.  Here are a few more puzzles to try:

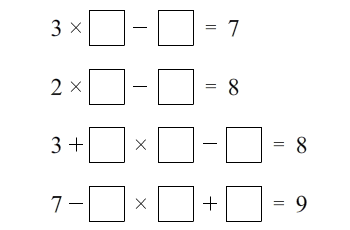
Good luck with the puzzles and pass them along to others who may enjoy them!

“There is no greatness where there is not simplicity, goodness, and truth.”
― Leo Tolstoy

Dividing by 5 mentally can be accomplished very easily. The best part is that there’s no division required. That’s right, there’s no division required to mentally divide a number by 5!  That sounds almost too good to be true.

All you need to do is multiply the number by 2 and then shift the decimal point left 1 place. That’s right, just two steps, multiplying by 2 and then shifting the decimal point of the product. Let me put them in bullet format:

 step 1: multiply the number by 2

 step 2: shift the decimal point left 1 place
 

So, if you want to divide 120 by 5, just do the following:

So 120 ÷ 5 = 24.  That’s pretty easy, isn’t it?  Well, it’s easy if you can quickly multiply numbers by 2 mentally.  This is referred to as “doubling” a number and it’s the basis of a lot of mental arithmetic techniques.  So in order to mentally divide by 5, first master doubling numbers mentally.  Let’s look at another example using a decimal number instead of an integer.   To divide 3246.4 by 5, just do the following: 

So 3246.4 ÷ 5 = 649.28.  Again, that’s pretty easy, isn’t it?  You may be asking “Why does it work?”.  Well, 5 is equal to 10 ÷ 2.  So when dividing by 5, it’s equivalent to dividing by “10 ÷ 2″.  This in turn is equivalent to multiplying by 2 and then dividing by 10.  In our base 10 (decimal) number system, dividing by 10 can be accomplished by shifting the decimal point left 1 place.  There we have it, instead of dividing by 5, we can just double and shift.

Give it a try on some other problems.  Start with integers that are easy to double (like 111 or 234) to get the idea.  Once you’re comfortable with those problems try a bit more challenging problems (like 756 or 1867) which are more difficult to double. 

Remember, mastering doubling numbers mentally is the key.  Practice and master that first and then dividing by 5 mentally will come easily.  Check out my Mental Math Anti-Calculator where you can practice your doubling of numbers and dividing by 5 interactively.  Access will be free to everyone until the end of March.  After that, contact me and I can set up an account for you.  Good luck and remember to practice doubling.

“Three things cannot be long hidden: the sun, the moon, and the truth.” – Budda

A counterexample is an example that shows a statement is false. Counterexamples are very important as they can be used to disprove a proposition. For example, given the proposition: “All prime numbers are odd”, 2 serves as a counterexample that disproves the proposition. 2 is a prime number, but it is not odd. It is important to realize that although counterexamples can be used to disprove propositions, examples can not be used to prove propositions.

The Counterexample Game is really straight forward. Given a statement, say whether it’s TRUE or FALSE. If it’s FALSE, then give a counterexample that shows that the proposition is FALSE. What’s great about the Counterexample Game is that it gets you thinking. It’s a great quick game that can be used as a starter for a group (in a classroom environment) or rapid-fire with individuals. The other great feature is that the subject does not have to be math. It can be based on nearly all subjects. Make a statement and if it’s false, just ask for a counterexample.

Below is a five statement counterexample game. Within this game four of the five statements are FALSE, so only one is TRUE (so it doesn’t have a counterexample).

1. All of the state names in the United States contain the letter “e”.

2. All rectangles are squares.

3. All multiples of 3 are odd.

4. All multiples of 2 are even.

5. Connecting three unique dots will always make a triangle.

These statements are from varied subjects (spelling, geometry and arithmetic).  You can gear the statement(s) to the subject matter being reviewed or studied.  Regardless of the subject matter, make it fun.  Challenge the students to think beyond their immediate response.  “I don’t know” is not allowed – encourage thinking.  Reward originality and accomplishment. 

Good luck and have fun.  Please comment if you  like these.  I plan on generating more of these to be used in classrooms.

“Live in the moment … but don’t be led by the moment, or the people who belong to it.” – J. Aleksandr Wootton

Happy New Year to All! I hope all is well with everyone.  I’ve started the new puzzling year off in a big way.  I’ve switched the MathMaverick Blog to WordPress from Facebook. It is something that I’ve wanted to do for a while. Finally, I’ve gotten off the sofa and done it! Hopefully this will make it more accessible and consistent (there were many problems with Facebook Notes in 2013 that were out of my control).

To start 2014 off, here are some math riddles for you to ponder. They are original riddles and from my riddle book, Riddle-Me Math, available on amazon. Have fun with the riddles. Please share them with others and Good luck

1.
I am a funny number
as you will plainly see
for if you add me to myself
my digits sum to me.

What number am I?

2.
Cats have 4,
You have 2,
And I have 3.
What can I be?

3.
Laying on a table,
Seven coins I see
Can you tell me what they are
If their sum is 53?

4.
Although it may seem funny,
Some say that time is money.
So if a dollar were a century,
Then this would be a year.

Good luck with the riddles and in the new year. Please share these riddles, reply with a comment or like us on facebook.