 It’s that time of year again – March 14th – that’s right, it’s PI DAY! PI is an irrational number. No, that doesn’t mean it’s unreasonable. It means it’s not rational – that is PI can not be represented as a ratio of two integers. In other words, PI can not be represented as a fraction (where the numerator and denominator are integers). However, PI can be approximated as a fraction or a decimal number. Many know PI as 3.14 or 3.1415 or even 3.141592653 (knowing this many digits promotes one to dork status – but that’s alright by me). No matter how many digits, these are just approximates of PI, often well within given or acceptable tolerances. Computers have found decimal approximations of PI to over a trillion decimal places (I kid you not!). There are many very interesting properties associated with PI. One that I find the most intriguing is the following summation:
It’s that time of year again – March 14th – that’s right, it’s PI DAY! PI is an irrational number. No, that doesn’t mean it’s unreasonable. It means it’s not rational – that is PI can not be represented as a ratio of two integers. In other words, PI can not be represented as a fraction (where the numerator and denominator are integers). However, PI can be approximated as a fraction or a decimal number. Many know PI as 3.14 or 3.1415 or even 3.141592653 (knowing this many digits promotes one to dork status – but that’s alright by me). No matter how many digits, these are just approximates of PI, often well within given or acceptable tolerances. Computers have found decimal approximations of PI to over a trillion decimal places (I kid you not!). There are many very interesting properties associated with PI. One that I find the most intriguing is the following summation:
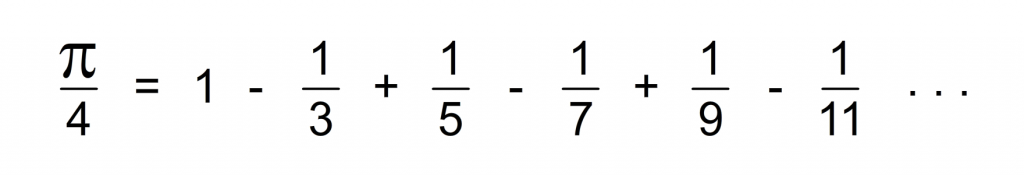 So multiplying the right side of the equation by 4 will result in an approximation of PI. Although PI can not be represented as a fraction, it can be found by infinitely adding and subtracting fractions (this is called an infinite summation). Even index terms are added and odd index terms are subtracted. Each term is just the reciprocal of 2n-1 (e.g. 1/(2n-1)) where n is any natural number. Initially, the summation does not show much promise. The sum of the first 12 terms is approximately 2.8952 – not very close to PI. However the sum of the first 200 terms is approximately 3.12159 – much closer! I have created a quick program that computes the approximate of PI based on the number of summations you input. Try 1000, 100000, 1000000 (a million) and 1000000000 (that’s a billion – it takes a few seconds) to see how the approximation converges towards PI.
So multiplying the right side of the equation by 4 will result in an approximation of PI. Although PI can not be represented as a fraction, it can be found by infinitely adding and subtracting fractions (this is called an infinite summation). Even index terms are added and odd index terms are subtracted. Each term is just the reciprocal of 2n-1 (e.g. 1/(2n-1)) where n is any natural number. Initially, the summation does not show much promise. The sum of the first 12 terms is approximately 2.8952 – not very close to PI. However the sum of the first 200 terms is approximately 3.12159 – much closer! I have created a quick program that computes the approximate of PI based on the number of summations you input. Try 1000, 100000, 1000000 (a million) and 1000000000 (that’s a billion – it takes a few seconds) to see how the approximation converges towards PI.
Have fun with PI and HAPPY PI DAY!

